들어가며: 동적 연결 관계 문제

여러 개의 노드와 그 사이를 잇는 간선으로 구성된 네트워크가 있다고 상상해 봅시다. 이때, “두 노드가 서로 연결되어 있는가?” 또는 “두 개의 분리된 그룹을 하나로 연결하라"와 같은 질의에 매우 효율적으로 답해야 하는 문제가 있습니다. 예를 들어, 소셜 네트워크에서 두 사람이 친구 관계인지(직접 또는 간접적으로) 확인하거나, 여러 컴퓨터 클러스터를 하나의 네트워크로 통합하는 상황이 여기에 해당합니다.

Union-Find 는 바로 이러한 동적 연결 관계(Dynamic Connectivity) 문제를 해결하기 위해 특화된 자료구조입니다. 서로소 집합(Disjoint Set) 또는 병합-찾기 집합(Merge-Find Set) 이라고도 불리며, 이름에서 알 수 있듯이 Union(집합 병합) 과 Find(루트 찾기) 라는 두 가지 핵심 연산을 제공합니다.

핵심 개념

Union-Find 자료구조는 서로 중복되는 원소가 없는 여러 개의 집합(서로소 집합)을 관리합니다. 이 집합들은 보통 트리의 숲(a forest of trees) 형태로 표현되며, 각 트리가 하나의 집합을 나타냅니다.

  • 대표자(Representative): 각 집합은 그 집합을 대표하는 고유한 멤버를 가집니다. 트리 구조에서는 루트(root) 노드 가 바로 그 집합의 대표자가 됩니다.
  • 부모 배열(Parent Array): Union-Find를 구현하는 가장 일반적인 방법은 1차원 배열(예: parent[])을 사용하는 것입니다. parent[i]는 원소 i의 부모 노드를 저장합니다. 만약 parent[i]가 자기 자신을 가리키거나 특별한 값(예: -1)을 가지면, 그 노드가 바로 트리의 루트이자 집합의 대표자입니다.

초기 상태: N개의 원소가 있다면, 처음에는 N개의 독립된 집합, 즉 N개의 노드가 각각 자기 자신을 루트로 하는 N개의 트리로 시작합니다. {1}, {2}, {3}, {4}, {5}, {6}, {7}, {8}

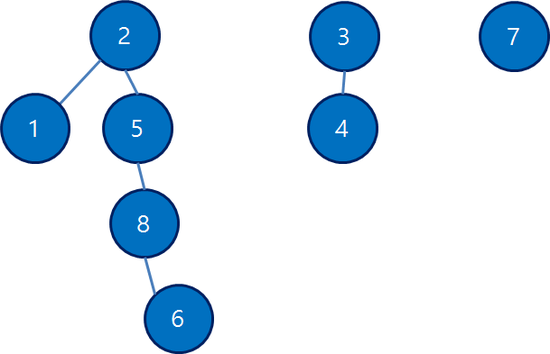
연산 후 상태: 몇 번의 union 연산이 수행되면, 아래 그림과 같이 여러 개의 트리가 숲을 이루는 형태로 집합들이 병합됩니다. {1, 2, 5, 6, 8}, {3, 4}, {7}

find 연산: 우리 대표가 누구야?

find 연산은 특정 원소가 어떤 집합에 속해 있는지, 즉 그 집합의 대표자(루트)가 누구인지 찾아주는 역할을 합니다. 두 원소 a와 b가 같은 집합에 속해 있는지 확인하려면, find(a)와 find(b)의 결과가 같은지 비교하면 됩니다.

기본 find 구현 

// parent[] 배열: parent[i]는 i의 부모 노드를 저장.
// 루트 노드는 parent[i] == i 또는 parent[i] < 0 등으로 표현.

int find(int n) {
    if (parent[n] == n) { // 자신이 루트 노드인 경우
        return n;
    }
    // 재귀적으로 부모를 따라 올라가 루트를 찾음
    return find(parent[n]);
}

이 구현은 간단하지만, 트리가 한쪽으로 긴 사슬 형태로 만들어지면(예: 1-2-3-4-5), find(5)를 호출할 때 O(N)의 시간이 걸리는 비효율이 발생합니다.

최적화 1: 경로 압축 (Path Compression)

이러한 비효율을 해결하기 위한 강력한 최적화 기법이 바로 경로 압축 입니다. find 연산을 수행하며 루트를 찾아 올라가는 과정에서 만나는 모든 노드들이 직접 루트를 가리키도록 갱신하는 것입니다.

int find(int n) {
    if (parent[n] == n) {
        return n;
    }
    // 재귀 호출에서 반환된 최종 루트를 자신의 부모로 직접 설정
    return parent[n] = find(parent[n]);
}

경로 압축을 적용하면, 한 번의 find 연산만으로도 트리의 높이가 극적으로 낮아져 평평한 형태로 변합니다. 따라서 이후의 find 연산은 거의 O(1)에 가까운 속도로 수행됩니다.

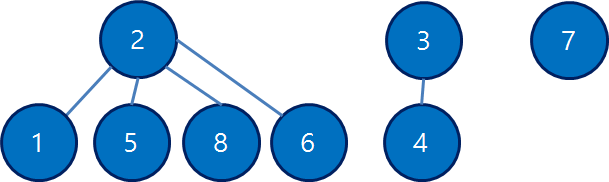경로 압축 후, 노드 6, 8, 5가 모두 루트 1을 직접 가리키게 된 모습

union 연산: 두 집합을 하나로

union 연산은 두 원소가 속한 집합을 하나의 집합으로 합치는 작업을 수행합니다.

기본 union 구현 

void union(int a, int b) {
    int rootA = find(a); // a의 루트 찾기
    int rootB = find(b); // b의 루트 찾기

    if (rootA != rootB) { // 두 원소가 서로 다른 집합에 속해 있다면
        parent[rootB] = rootA; // b의 루트를 a의 루트 자식으로 만듦
    }
}

이 구현 역시 간단하지만 문제가 있습니다. 키가 큰 트리(예: 높이 5)를 키가 작은 트리(예: 높이 2) 아래에 붙이면, 전체 트리의 높이가 불필요하게 깊어질 수 있습니다.

최적화 2: 랭크/크기 기반 합치기 (Union by Rank/Size)

트리가 깊어지는 것을 방지하기 위해, 두 트리를 합칠 때 일정한 규칙을 적용하는 최적화 기법입니다.

  • Union by Rank (랭크 기반): 각 트리의 높이(또는 랭크)를 기록해두고, 항상 높이가 낮은 트리를 높이가 높은 트리 아래에 붙입니다. 이렇게 하면 트리의 높이가 불필요하게 증가하는 것을 막을 수 있습니다.
  • Union by Size (크기 기반): 각 집합의 크기(원소의 개수)를 기록해두고, 항상 크기가 작은 집합을 크기가 큰 집합 아래에 붙입니다.

다음은 Union by Rank를 적용한 union 연산의 구현 예시입니다.

int[] rank = new int[N + 1]; // 각 노드의 랭크를 저장하는 배열

void union(int a, int b) {
    int rootA = find(a);
    int rootB = find(b);

    if (rootA != rootB) {
        // 랭크가 더 높은 쪽을 루트로 삼는다
        if (rank[rootA] < rank[rootB]) {
            parent[rootA] = rootB;
        } else if (rank[rootA] > rank[rootB]) {
            parent[rootB] = rootA;
        } else { // 랭크가 같다면
            parent[rootB] = rootA;
            rank[rootA]++; // 랭크를 1 증가시킨다
        }
    }
}

시간 복잡도 분석

Union-Find 자료구조의 진정한 힘은 시간 복잡도에 있습니다.

  • 기본 구현: 최악의 경우 O(N)
  • 경로 압축 과 Union by Rank/Size 최적화를 모두 적용 했을 때, M개의 연산에 대한 시간 복잡도는 O(M * α(N)) 입니다.

여기서 α(N) 은 역 아커만 함수(Inverse Ackermann Function) 로, 상상할 수 있는 모든 N값에 대해 5 미만의 값을 가지는, 증가 속도가 극도로 느린 함수입니다. 따라서 사실상 상수 시간(amortized constant time) 에 가깝다고 볼 수 있습니다.

결론

Union-Find는 서로소 집합을 다루고 원소들의 연결 관계를 추적하는 문제에 있어 거의 상수 시간에 가까운 압도적인 성능을 제공하는 자료구조입니다. 크루스칼 알고리즘(Kruskal’s Algorithm)에서 사이클 생성 여부를 확인하는 등 그래프 알고리즘에서도 널리 활용됩니다. 그 놀라운 효율성은 경로 압축 과 Union by Rank/Size 라는 두 가지 핵심적인 최적화 기법에서 비롯된다는 점을 기억하는 것이 중요합니다.